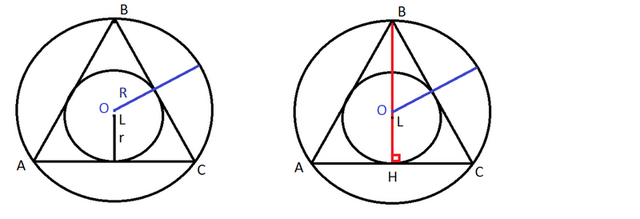
Во вложении рисунок:
O - центр описанной окружности около треугольника АВС
L - центр окружности, вписанной в треугольник АВС
BH - высота
Дано:
АВС - равнобедренный треугольник (АВ=ВС)
ВН - высота, ВН = 9
АС = 24
Найти: R и r
Решение:
BH - это высота, биссектриса и медиана, т.к. В равнобедренном треугольнике медиана, биссектриса и высота, проведенные к основанию, совпадают.
AH=HC=12
По Теореме Пифагора:



Есть такое свойство:
Если в многоугольник можно вписать окружность, то его площадь равна произведению полупериметра многоугольника на радиус этой окружности:
S = pr
P = 54,
p = 27
S = 27r
Есть еще одна формула:


S = 108
108 = 27r
r = 4
Найдем R:
Есть еще одна формула для нахождения площади треугольника:


S = 108
108 =

432R = 5400
R = 12,5
Ответ: r = 4, R = 12, 5