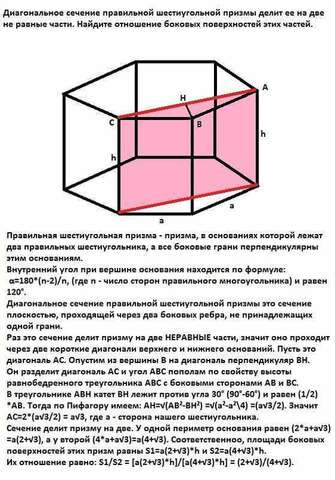
Правильная шестиугольная призма - призма, в основаниях которой лежат два правильных шестиугольника, а все боковые грани перпендикулярны этим основаниям.
Внутренний угол при вершине основания находится по формуле:
α=180*(n-2)/n, (где n - число сторон правильного многоугольника) и равен 120°.
Диагональное сечение правильной шестиугольной призмы это сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Раз это сечение делит призму на две НЕРАВНЫЕ части, значит оно проходит через две короткие диагонали верхнего и нижнего оснований. Пусть это диагональ АС. Опустим из вершины В на диагональ перпендикуляр ВН.
Он разделит диагональ АС и угол АВС пополам по свойству высоты равнобедренного треугольника АВС с боковыми сторонами АВ и ВС.
В треугольнике АВН катет ВН лежит против угла 30° (90°-60°) и равен (1/2)*АВ. Тогда по Пифагору имеем: АН=√(АВ²-ВН²) =√(а²-а²\4) =(а√3/2). Значит АС=2*(а√3/2) = а√3, где а - сторона нашего шестиугольника.
Сечение делит призму на две. У одной периметр основания равен (2*а+a√3)=a(2+√3), а у второй (4*а+a√3)=a(4+√3). Соответственноо, площади боковых поверхностей этих призм равны S1=a(2+√3)*h и S2=a(4+√3)*h.
Их отношение равно: S1/S2 = [a(2+√3)*h]/[a(4+√3)*h] = (2+√3)/(4+√3).