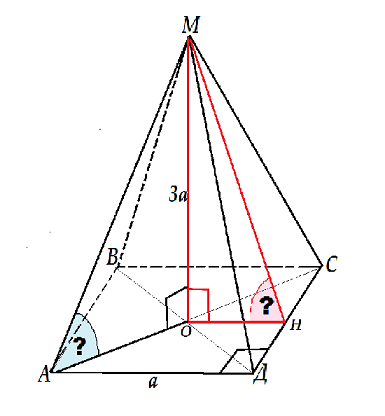
В правильной четырехугольной пирамиде сторона основания равна a, а высота 3a . Найдите углы наклона боковых ребер и боковых граней к плоскости основания.Сделаем рисунок пирамиды МАВСД.
Т.к. пирамида правильная, основание высоты МО совпадает с центром вписанной в основание окружности.
МО⊥АВСД.
МО=3а, АД=а, АО=ОС.
Искомые углы - это углы МНО и МАО.
ОН=АД:2=а/2
tg∠МНО=МО:ОН=3а: 0,5а=6
По таблице тангенсов это тангенс угла 80°30’
tg∠МАО=МО:ОА
ОА=АС:2
АС=а√2 ( как диагональ квадрата)
ОА=(а√2):2
tg∠МАО=3а:[(а√2):2] ≈ 4,243
По таблице тангенсов это тангенс угла 76°42'