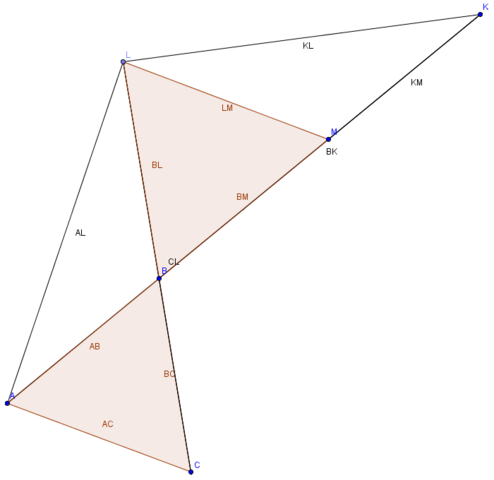
Треугольник ABC правильный (по условию), следовательно:
AB = BC = AC,
Углы ABC, BAC и BCA равны 60 градусам.
Углы LBM и ABC вертикальные, следовательно угол LBM равен углу ABC и равен 60 градусам.
На продолжении стороны AB за точку B отметим точку M так, чтобы угол LMB был равен 60 градусам.
Рассмотрим получившийся треугольник BLM:
Угол BLM = 180 - угол LBM - угол LMB = 180 - 60 - 60 = 60
Мы нашли, что все три угла треугольника BLM равны 60 градусам, следовательно он правильный, следовательно BL = BM = LM.
AL = KL (по условию), следовательно треугольник ALK равнобедренный, следовательно угол LAB равен углу LKM.
Углы LBA и LBM смежные, следовательно угол LBA = 180 - угол LBM
Углы LMK и LMB смежные, следовательно угол LMK = 180 - угол LMB
Мы знаем, что угол LBM равен углу LMB, следовательно угол LBA равен углу LMK.
Угол ALB = 180 - угол LAB - угол LBA (сумма углов треугольника 180)
Угол KLM = 180 - угол LKM - угол LMK (сумма углов треугольника 180)
Угол LAB равен углу LKM и угол LBA равен углу LMK, следовательно угол ALB равен углу KLM.
Мы знаем, что AL = KL, BL = LM и угол LBM равен углу LMB, следовательно треугольники ABL и KLM равны, по первому признаку равенства треугольников, следовательно AB = KM.
AB = BC и AB = KM, следовательно BC = KM.
Точка B делит отрезок CL на два отрезка, следовательно CL = BC + BL
Точка M делит отрезок BK на два отрезка, следовательно BK = BM + KM
Мы знаем, что BL = BM и BC = KM, следовательно CL = BK.
Доказано.