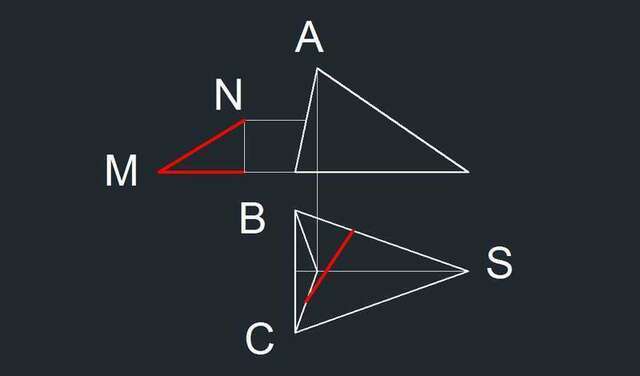
Так как требуется узнать угол между прямой MN и плоскостью BSC, то повернём заданную пирамиду так, чтобы эта плоскость была её основанием.
Примем систему координат с нулём в точке К - это середина стороны ВС, через точку S - ось у, через точку С - ось х и вертикальная ось - z.
Рассмотрим треугольник KAS в осевом сечении пирамиды.
Сторона КА = √(2²-(2/2)²) = √3 =
1.732051.
Сторона KS = √(3²-(2/2)²) = √8 = 2.828427.
Найдем высоту из точки А - это будет координата z этой точки:
ha =2√(p(p-a)(p-b)(p-c))/a = 1.695582.
Здесь р - полупериметр, р = 3.780239.
По теореме косинусов определим косинус угла ASK:
cos ASK = (a²+b²-c²)/(2ab) = (3²+(√8)²-(√3)²)/(2*3*√8) =
(14/6√8) = 0.82496.
Основание высоты из точки А обозначим Е.
Тогда расстояние КЕ = √8-3*cos ASK = √8-3*0,82496 = 0,353553.
Определим координаты вершин пирамиды:
С(1;0;0) В(-1;0;0) S(0;2.82842;0) А(0;,353553;1.695582).
Теперь переходим к координатам точек M и N.
Координаты точки N являются средними между точками С и А:
N(0,5;0,176777;0,847791).
Координаты точки M находим по формуле деления отрезка в заданном соотношении λ:
х = (х₁+λх₂)/(1+λ), по такой же формуле y и z.
М(-0,666667;0,942809;0)
Находим длину отрезка MN по формуле
d =√ ((х₂ - х₁ )² + (у₂ - у₁ )² + (z₂ – z₁ )²):
MN =
0.5
0.176777
0.847791
-0.66667
0.942809
0 = 1.632993
Углом между прямой и плоскостью называется угол, образованный прямой и её проекцией на плоскость.
Длину проекции на плоскость найдем по предыдущей формуле, исключив вертикальную координату точки N:
.MN₁ =
0.5
0.176777
0
-0.66667
0.942809
0 = 1.395678.
Отсюда косинус искомого угла равен:
cos α = 1.395678 / 1.632993 =
0.854675
α = 0.545872 радиан = 31.2762°.