Допустим, что некое x=k является корнем. Тогда x=-k тоже является корнем, т.к. икс везде либо в квадрате, либо под отдельным модулем. Следовательно, если корень - единственный, то он равен 0. Чтобы узнать, при каких а 0 является корнем (не факт, что единственным), нужно подставить вместо x 0.

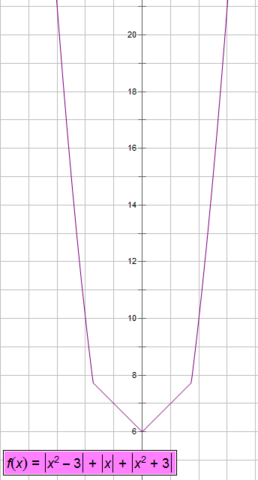
Отсюда следует, что условие может выполняться только при |a|=3. Однако если подставить a=3 в уравнение и построить график левой части, то будет видно, что при х=0 значение минимально и равно правой части, а сам график похож на обрезанную параболу, то есть других корней нет.
Ответ: