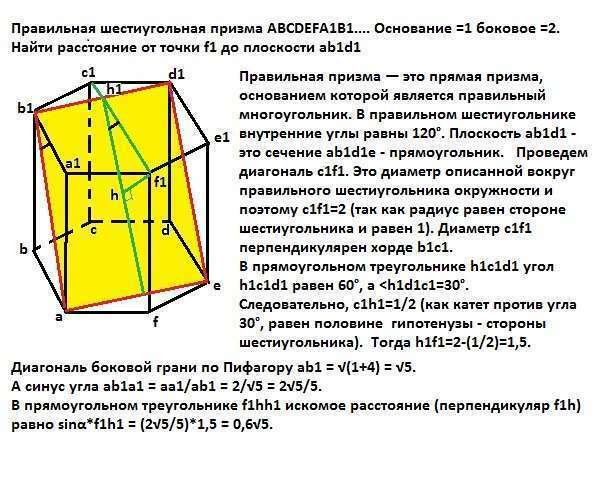
Правильная призма — это прямая призма, основанием которой является правильный многоугольник. В правильном шестиугольнике внутренние углы равны 120°. Плоскость ab1d1 - это сечение ab1d1e - прямоугольник. Проведем диагональ с1f1. Это диаметр описанной вокруг правильного шестиугольника окружности и поэтому c1f1=2 (так как радиус равен стороне шестиугольника и равен 1). Диаметр c1f1 перпендикулярен хорде b1c1.
В прямоугольном треугольнике h1c1d1 угол h1c1d1 равен 60°, а Следовательно, c1h1=1/2 (как катет против угла 30°, равен половине гипотенузы - стороны шестиугольника). Тогда h1f1=2-(1/2)=1,5.
Диагональ боковой грани по Пифагору ab1 = √(1+4) = √5.
А синус угла ab1a1 = aa1/ab1 = 2/√5 = 2√5/5.
В прямоугольном треугольнике f1hh1 искомое расстояние (перпендикуляр f1h) равно sinα*f1h1 = (2√5/5)*1,5 = 0,6√5.
Ответ: расстояние от точки f1 до плоскости ab1d1 равно 0,6√5.