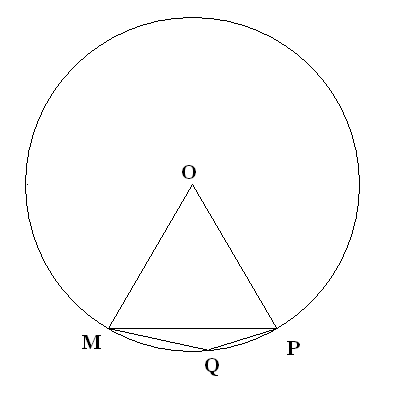
2. (см. рис.)
Проведём радиусы OM и OP. По условию OM = OP = MP, значит треугольник MOP - равносторонний, и все его углы равны 60 градусов.
Тогда большой угол MOP (проходящий через верхнюю часть окружности) равен 360-60 = 300 градусов.
Угол MQP (искомый угол Q) является вписанным. Он опирается на бОльшую дугу MP. Больший угол MOP является центральным.
По определению величина вписанного угла равна половине центрального угла, опирающегося на ту же же дугу, т.е.