х^3+х^2-8х-12>0
1. Для начала, разложим его на множетели.
Для этого разделим это равнение, на одно из его корней, корни надо искать среди делителей свободного члена(12)
+-1;+-2;+-3;+-4;+-6;+-12;
Подставим например -2
-8+4+16-12=0
0=0 - поддходит
Тперь делим(деление смотри в приложениях)
Получили
х^3+х^2-8х-12=(x+2)(x^2-x-6)
2. Еще раз разложим квадратное уравнение
x^2-x-6=0
D=1+24=25
x1=1+5/2=3;
x2=1-5/2=-2
И того:
х^3+х^2-8х-12=(x+2)(x-3)(x+2)
(x+2)(x-3)(x+2)>0
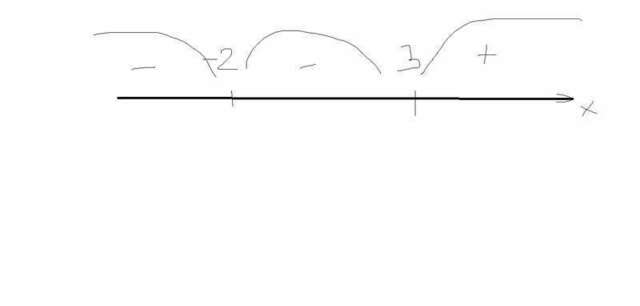
Решаем методом интервалов(решение сморти в приложениях)
(главное правильно раставить знаки)
И того Ответ: x(принадлежит) (3;+бесконечности)