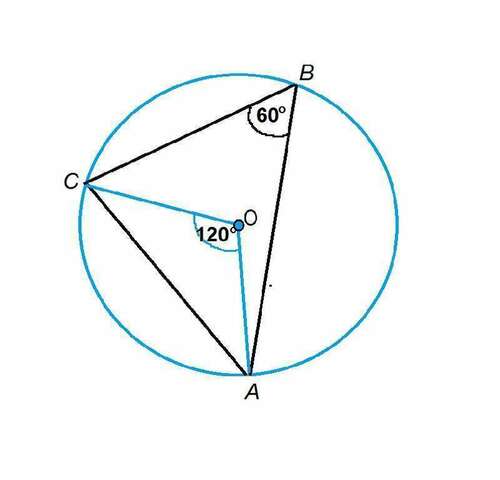
Точки АВС лежат на окружности. Значит, соединив их, получим вписанный треугольник АВС.
Так как вписанный угол В=60°, опирающийся на ту же дугу
центральный угол СОА=60*2=120°, и на дугу СВА приходится 360°-120°=240° от всей окружности.
Примем коэффициент отношения величины дуг АВ:ВС за х, тогда
АВ=7х, ВС=5х, их сумма = 12 х
На х приходится
240°:12=20°
Вписанный угол равен половине градусной меры центрального угла, который опирается на ту же дугу.
Центральные угол СОВ=20°*5=100°, вписанный САВ=100°:2=50°;
центральный угол ВСО=20°*7=140°, вписанный ВСА=140°:2=70°
Сумма вписанных углов треугольника АВС=60°+50°+70°=180°, как и положено каждому треугольнику.