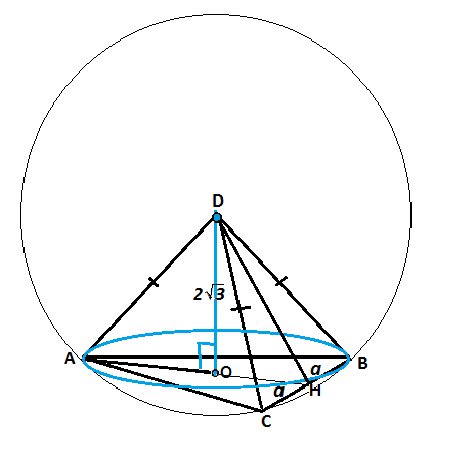
В правильной треугольной пирамиде DABC боковые ребра DA,DB и DC взаимно перпендикулярны. Вершина D является центром сферы , на поверхности которой лежат точки A,B, и C. Найдите площадь сферы, если ее высота равна 2√3 см.
-------
Понятно, что 2√3 см - высота пирамиды, т.к. у сферы нет высоты.
-------------
Боковые ребра пирамиды взаимно перпендикулярны, вершины ∆ АВС лежат на поверхности сферы, D- ее центр, следовательно, все ребра данной пирамиды равны радиусу R сферы, и боковые грани - равнобедренные прямоугольные треугольники/
Боковые ребра пирамиды равны, ⇒ равны их проекции на плоскость треугольника АВС, ⇒ основание О высоты DО лежит в центре описанной вокруг ∆ АВС окружности.
Пусть стороны основания равны 2а.
Высота DH боковой грани делит ее на два равнобедренных прямоугольных треугольника, является её медианой и равна половине стороны основания. DH=a ⇒
R сферы =AD
АD = DС=
a√2 как гипотенуза равнобедренного прямоугольного треугольника DHC.
AO=2a /√3 как радиус описанной вокруг ∆ АВС окружности.
AD²=OD²+AO²
(a√2)²=(2√3)²+(2a/√3)²
2a²=12+(4a²/3)
6a²=36+4a²
2a²=36
AD²=36=
R²
Sсферы=4πR²
S=4*36π=144π см²