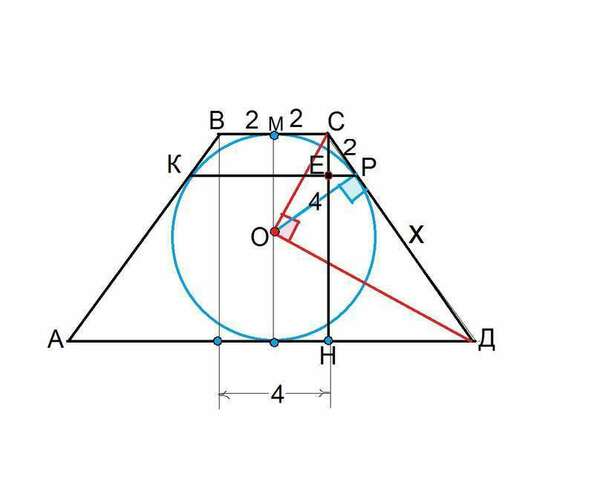
Одно из оснований равнобедренной трапеции равно 4. Найдите расстояние между точками касания с ее боковыми сторонами вписанной в трапецию окружности радиуса 4.
РЕШЕНИЕ
Ясно, что 4 равно меньшее основание - большее не может быть меньше диаметра вписанной окружности.
В равнобедренная трапеция АВСД основание ВС=4, r ω=4, ⇒
высота СН=2r=8,
СР=СМ=2 по свойству отрезков касательных из одной точки.
Сумма углов трапеции, прилежащих к одной боковой стороне, равна 180°
Центр вписанной окружности лежит на пересечении биссектрис углов трапеции, ⇒
угол СОД=полусумме этих углов и равен 90°
ОР - высота прямоугольного треугольника СОД и равна r=4
Высота прямоугольного треугольника есть среднее пропорциональное отрезков, на которые она делит гипотенузу:
ОР²=СР*РД
16=2*РД
РД=16:2=
8
В прямоугольном треугольнике СНД высота СН=2r=8, гипотенуза СД=2+8=10,
треугольник СОД «египетский» и
НД=6 ( можно проверить по т.Пифагора)
КР|| основаниям трапеции, т.к. точки касания находятся на равном от них расстоянии.
Δ СЕР ≈ Δ СНД по двум углам - прямому и общему острому.
Тогда
СР:СД=ЕР:НД
2:10=ЕР:6
10 ЕР=12
ЕР=12:10=
1,2
Половина КР= половине ВС +ЕР=2+1,2=
3,2
КР=3,2*2=6,4