Если под плоскостью а понимать плоскость, проходящая по нижней части шаров, то решение будет таким:
Оси шаров образуют равносторонний треугольник со стороной 2R.
Расстояние в плане от оси шара до оси конуса (обозначим его АО) равно 2/3 высоты (она же и медиана) этого треугольника.
АО = (2/3)*(2R√3)/2) = 2R√3 / 3 = 2R / √3.
Проведём сечение по оси одного их шаров и по оси конуса.
Расстояние от оси шара до образующей конуса равно R*tg(90-ф)/2).
Расстояние от образующей до оси конуса (радиус конуса) равно:
(2R / √3) - R*tg(90-ф)/2).
Отсюда искомая величина (это высота конуса до основания шаров) равна ((2R / √3) - R*tg(90-ф)/2)) / tg Ф.
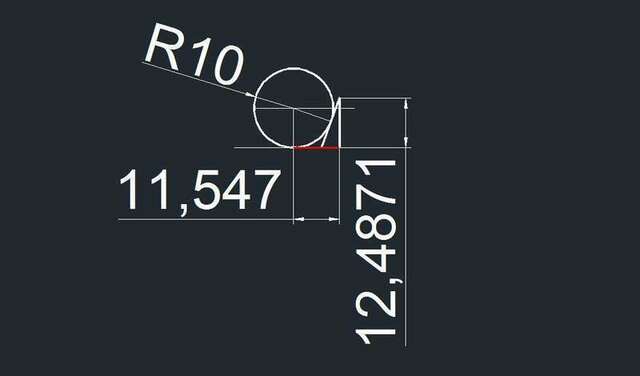
Для примера приводится чертёж с разрезом по оси шара радиусом 10 и углом Ф=20°.
√3 = 1.732051
R/V3*tgφ= 15.86257
2-V3*ctg(φ/2) =0.787204968
=
12.48709
2R/V3 =
11.5470.