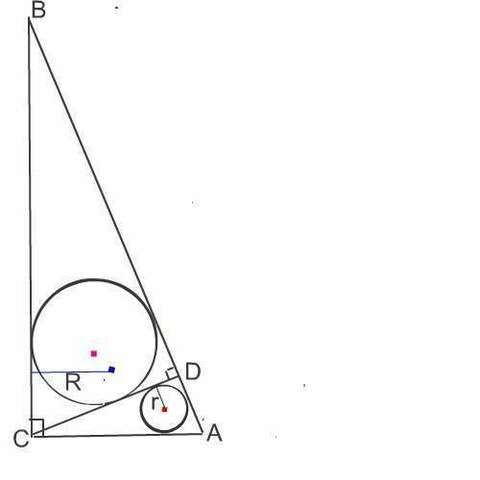
Сделаем рисунок к задаче.
Δ АВС, Δ АСD и Δ ВСDподобны по свойству высоты прямоугольного треугольника, проведенной из прямого угла к гипотенузе.
Для удобства при вычислениях обозначим
длину АD равной х,
длину СD равной у.
Из подобия треугольников АСD и ВСD:
х:5=у:12,
По свойству пропорции: произведение средних членов пропорции равно произведению ее крайних членов:
5у=12х
отсюда
у=12х/5.
Найдем АС из треугольника АСD по теореме Пифагора:
AC²=x²+y²
AC²=x²+144x²/25
AC =√(x²+144x²/25)=13x/5
Обозначим искомый радиус вписанной в треугольник АВС окружности R
Составим пропорцию отношения радиусов R и r вписанных окружностей и меньших катетовв подобных треугольниках АВС и АСD
R:5=АС:х
R:5=(13x/5):х
Rх=5(13x/5)
R = 13 см