1. Область определения функции

- множество всех действительных чисел
2. Четность функции
y(-x)=y(x) - функция четная
у(-х)=-у(х) - нечетная

3. Точки пересечения с осью Ох и Оу
3.1. С осью Ох


- точки пересечения с осью Ох
3.2. С осью Оу


- точки пересечения с осью Оу
Функция нечетная...........
4. Точки экстремумы, возрастание и убывание
4.1 Первая производная

4.2. Точки экстремумы

4.3 Возрастание и убывание функции
_____-____(-0,5)____+___(0,5)___-_____>
Итак, функция убывает на промежутке

, возрастает на промежутке

. В точке х=-0,5 функия имеет локальный минимум, а в точке х=0,5 - локальный максимум
5. Точки перегиба
5.1. Вторая производная

Приравняем к нулю

___+___(0)___-____>
(-∞;0) вогнута вверх, а (0;+∞) - вогнута вниз
Вертикальные асимптоты нет
Горизонтальных асимптот нет
Наклонных асимптот нет
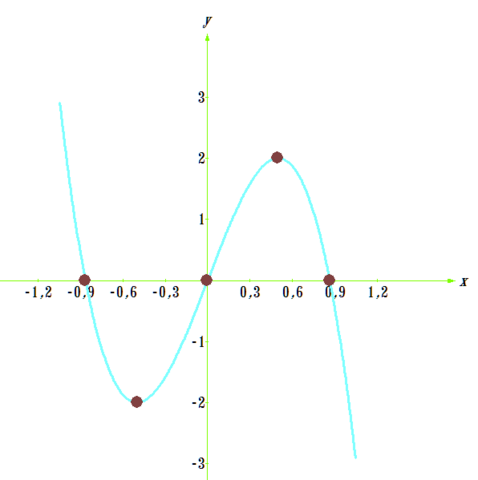
График смотрите во вложении