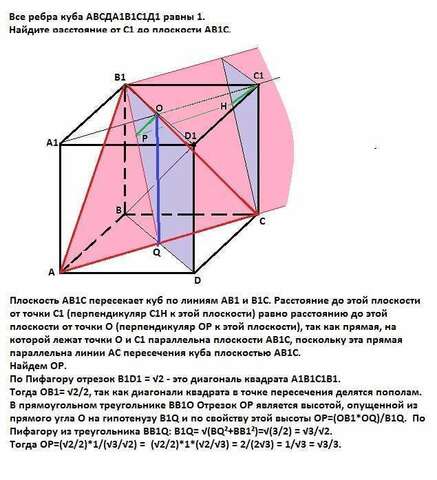
Плоскость АВ1С пересекает куб по линиям АВ1 и В1С. Расстояние до этой плоскости от точки С1 (перпендикуляр С1Н к этой плоскости) равно расстоянию до этой плоскости от точки О (перпендикуляр ОР к этой плоскости), так как прямая, на которой лежат точки О и С1 параллельна плоскости АВ1С, поскольку эта прямая параллельна линии АС пересечения куба плоскостью АВ1С.
Найдем ОР.
По Пифагору отрезок В1D1 = √2 - это диагональ квадрата А1В1С1В1.
Тогда ОВ1= √2/2, так как диагонали квадрата в точке пересечения делятся пополам.
В прямоугольном треугольнике ВВ1О Отрезок ОР является высотой, опущенной из прямого угла О на гипотенузу В1Q и по свойству этой высоты OP=(ОВ1*ОQ)/В1Q. По Пифагору из треугольника ВВ1Q: В1Q= √(BQ²+ВВ1²)=√(3/2) = √3/√2.
Тогда ОР=(√2/2)*1/(√3/√2) = (√2/2)*1*(√2/√3) = 2/(2√3) = 1/√3 = √3/3.
Ответ: расстояние от С1 до плоскости АВ1С равно √3/3.