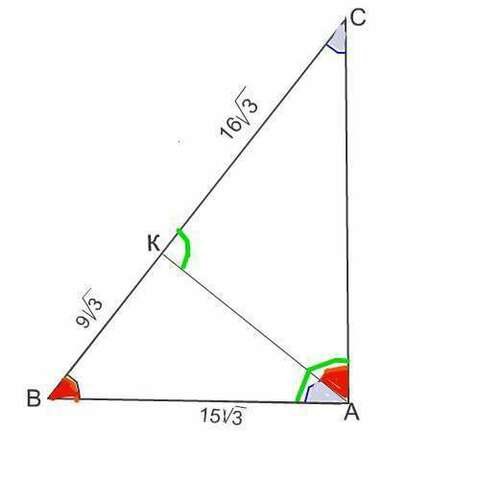
Рассмотрим Δ КСА и Δ ВКА
Из подобия ( по условию задачи) Δ КСА и Δ АВС ∠ АКС= ∠ ВАС, ∠ КАС = ∠ КВА
∠ СКА с ∠ ВКА образует угол в 180 градусов. Следовательно, ∠ ВКА равен сумме
∠ КСА и ∠ КАС. ⇒∠ ВКА=90 °, из чего следует, что Δ АВС прямоугольный и КА в нем высота.
Из отношения сторон в треугольнике АВС и ВКА
ВС:АВ =АВ:ВК равны 25√3:15√3=5:3 следует, что три стороны этих прямоугольных треугольников относятся как 3:4:5.Отсюда сторона АК=12√3, а площадь треугольника КАС равна половине произведения его катетов
S КАC=16√3*12√3=16*12*3=576 см²