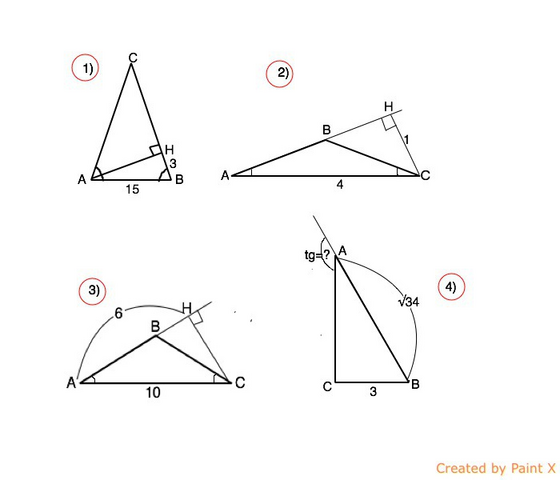
1) В треугольнике ABC AC=BC, АB=15, АН- высота; BH=3. Найдите cos А
АС=ВС, ⇒ ∆ АВС - равнобедренный и ∠А=∠В, значит, cos A=cos B
cos B=HB:AB=3/15=0,2
2) В треугольнике ABC AB=BC, AC=4, высота CH равна 1. Найдите синус угла ACB
∆ АВС - равнобедренный. ⇒∠А=∠С, и синус ∠АСВ=синусу ∠СAВ
sin ∠CAB=CH:AC=1/4=0,25
3) В тупоугольном треугольнике ABC AB=BC, AC=10, CH-высота, AH=6. Найдите sin ACB
Т.к. ∆ АВС равнобедренный, углы при основании АС равны, следовательно, равны их синусы.
sinBAC=CH:AC
По т.Пифагора СН=√(AC²-AH²)=√(100-36)=8
sinBAC=8/10=0,8 ⇒sin ACB=0,8
(Замечу, что задача не совсем корректна. Т.к. треугольник тупоугольный, высота из острого угла - вне треугольника. И СН не может быть больше наклонной ВС, тем более не может быть больше АВ+ВН, если АВ=ВС. Возможно, нужно было длину АН обозначить равной 8 или АС=ВС)
4) В треугольнике ABC угол C равен 90 градусов , AB=корень из 34, BC=3. Найдите тангенс внешнего угла при вершине A
Внешний угол при вершине А - смежный внутреннему углу при той же вершине. Тангенсы смежных углов равны по величине, но имеют противоположные знаки.
tg CAB=BC:AC
АС по т.Пифагора =√(АВ-CB)=√(34-9)=5
CAB=3/5=0,6⇒ тангенс внешнего угла при вершине А= -0,6