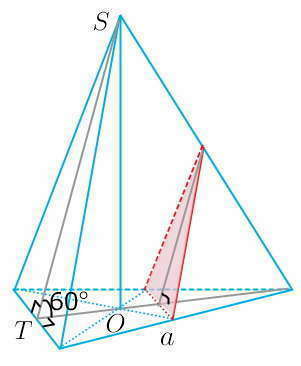
Пирамида правильная:
основание -- равносторонний треугольник
боковые грани -- равнобедренные треугольники
сечение -- равнобедренный треугольник с основанием = (a/2),
подобный боковой грани с коэффициентом (1/2), т.к. его боковые стороны тоже являются средними линиями соотв.треугольников
апофема ST = 2*TO, т.к. угол STO=60 градусов по условию
ТО -- это треть высоты (медианы) основания
высота равностороннего треугольника = a√3 / 2
TO = a√3 / 6
ST = a√3 / 3
высота сечения = a√3 / 6
площадь сечения = a² √3 / 24