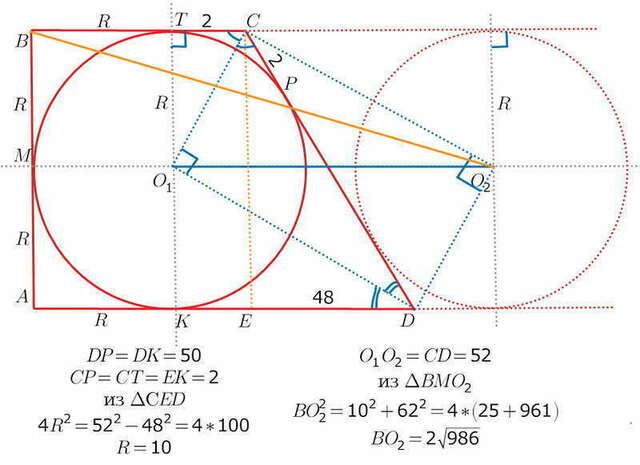
Окружности будут равные, т.к. их диаметры равны, как отрезки параллельных прямых, заключенные между параллельными основаниями трапеции))
центры окружностей расположены на биссектрисах соотв углов: CO1, DO1, CO2, DO2
CO1 _|_ DO1 как биссектрисы углов, сумма которых = 180 градусов)))
аналогично CO2 _|_ DO2
CO2DO1 --прямоугольник, диагонали прямоугольника равны: CD=O1O2
радиус окружностей можно найти из прямоугольного треугольника, построив еще одну высоту трапеции)))
отрезки касательных к окружности, проведенных из одной точки, равны)))