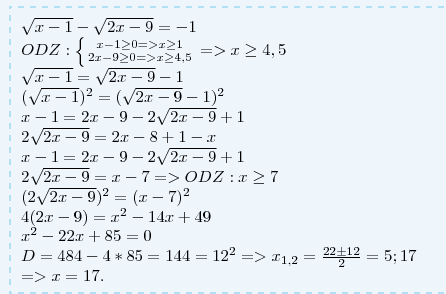x \geq 1} \atop {2x-9 \geq 0=>x \geq 4,5}} \right. => x \geq 4,5 \\ \sqrt{x-1} =\sqrt{2x-9}-1 \\ (\sqrt{x-1})^2 =(\sqrt{2x-9}-1)^2 \\
x-1=2x-9-2\sqrt{2x-9}+1 \\ 2\sqrt{2x-9}=2x-8+1-x \\ x-1=2x-9-2\sqrt{2x-9}+1 \\ 2\sqrt{2x-9}=x-7=> ODZ:x \geq 7 \\ (2\sqrt{2x-9})^2=(x-7)^2 \\ 4(2x-9)=x^2-14x+49 \\ x^{2} -22x+85=0 \\ D=484-4*85=144=12^2 => x_{1,2}= \frac{22 \pm 12}{2}=5;17 \\ =>x= 17." alt="\sqrt{x-1} - \sqrt{2x-9}=-1 \\ ODZ: \left \{ {{x-1 \geq 0=>x \geq 1} \atop {2x-9 \geq 0=>x \geq 4,5}} \right. => x \geq 4,5 \\ \sqrt{x-1} =\sqrt{2x-9}-1 \\ (\sqrt{x-1})^2 =(\sqrt{2x-9}-1)^2 \\
x-1=2x-9-2\sqrt{2x-9}+1 \\ 2\sqrt{2x-9}=2x-8+1-x \\ x-1=2x-9-2\sqrt{2x-9}+1 \\ 2\sqrt{2x-9}=x-7=> ODZ:x \geq 7 \\ (2\sqrt{2x-9})^2=(x-7)^2 \\ 4(2x-9)=x^2-14x+49 \\ x^{2} -22x+85=0 \\ D=484-4*85=144=12^2 => x_{1,2}= \frac{22 \pm 12}{2}=5;17 \\ =>x= 17." align="absmiddle" class="latex-formula">
Ответ: х=17.