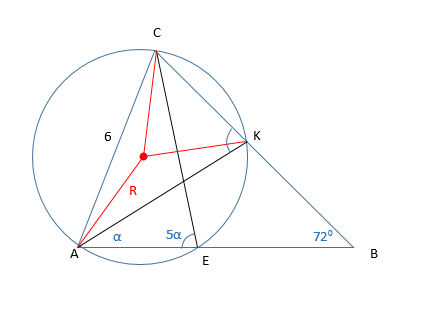
Выполним построение.
Углы AEC и AKC вписаны в окружность и опираются на одну и ту же дугу. Значит, они равны между собой.
Угол АКС является внешним углом треугольника АКВ. Следовательно, он равен сумме двух других углов треугольника, не смежных с ним:
5α=α+72°
4α=72°
α=18°
Данная окружность описана вокруг треугольника АСК. По формуле радиуса описанной окружности, получаем:

Ответ: 3