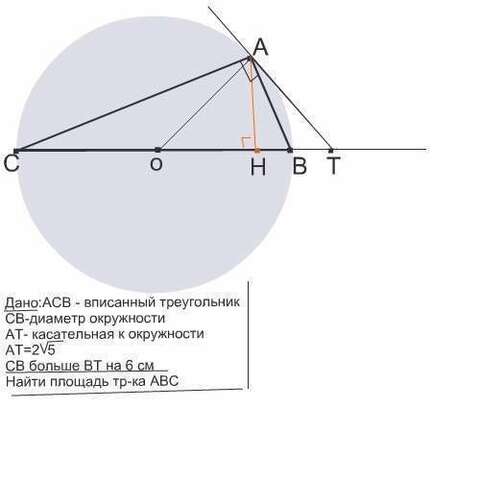
Этот треугольник прямоугольный, т.к. его гипотенуза является диаметром окружности.
Площадь треугольника находим обычным способом
S=половина произведения высоты на основание.
Но мы не знаем ни высоты, ни основания треугольника АВС.
Соединим центр окружности с вершиной А треугольника АВС.
Примем радиусы окружности СО, ОВ, ОА равными х.
Тогда
диаметр СВ=2х, а ВТ=2х-6
СТ=ВТ+2х=(2х-6)+2х=4х-6
Отрезок ОТ=4х-6-х=3х-6
Из треугольника АОТ найдем по теореме Пифагора значение х:
АО²=ОТ²-АТ²
х²=(3х-6)²-(2,5)²
х²=9х²-36х+36 -20
8х²-36х+16=0
Решив квадратное уравнение, найдем
х=4. ( второй корень (-0,5) не подходит и по знаку, и по величине)
R=х=4,
диаметр окружности (гипотенуза треугольника АВС) равен 2R=8.
Так как ВС по условию задачи больше ВТ на 6 см,
ВТ=8-6=2 см
Треугольник АОТ - прямоугольный (по свойству касательной ), катеты в нем 4 и 2√5, гипотенуза равна ОВ+2=6
Необходимо найти высоту h этого треугольника, которая является высотой и треугольника АВС, чтобы ответить на основной вопрос задачи.
Обозначим точку высоты на ОТ буквой Н.
h=АО²-ОН² и h=АТ²- НТ²⇒ 4²-ОН²=20-(6-ОН)²
16 - ОН²=20 - 36+12ОН-ОН²
16-20+36=12ОН
12ОН=32 3ОН=8
ОН=8/3
h²=16 - 64/9
9h²=144 - 64=80
h²=80/9
h=√80/9=√(16*5/9)=(4√5):3
S АВС=0,5* 8*(4√5):3 =(16√5):3