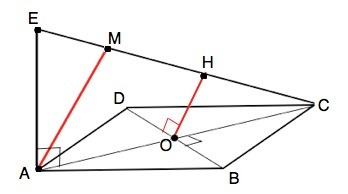
Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
ЕА перпендикулярна плоскости квадрата, ⇒
плоскость АЕС перпендикулярна плоскости квадрата.
АМ пересекает плоскость АВСD в точке, не принадлежащей BD.
Прямые АМ и BD лежат в разных плоскостях, не параллельны и не пересекаются. Эти прямые -
скрещивающиеся.
Чтобы найти угол между скрещивающимися прямыми, нужно провести прямую, параллельную одной них так, чтобы она пересекала вторую прямую. При этом получаются пересекающиеся прямые. Угол между ними равен углу между исходными скрещивающимися прямыми.
Диагонали квадрата пересекаются под прямым углом.
Проведем в плоскости АЕС через точку пересечения диагоналей О наклонную ОН параллельно АМ. Проекция ОН принадлежит АС и перпендикулярна ВD.
По т. о 3-х перпендикулярах ВD перпендикулярна ОН. Следовательно, ВD перпендикулярна АМ.
Угол между ВD и АМ равен
90°.