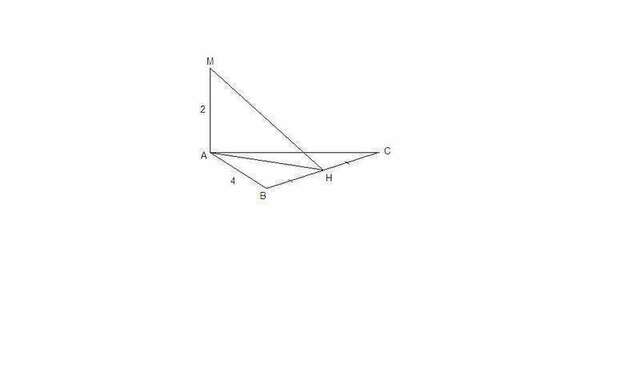
Пусть Н - середина ВС.
Тогда АН медиана и высота правильного ΔАВС,
АН⊥ВС.
АН - проекция МН на плоскость АВС, ⇒
МН⊥ВС по теореме о трех перпендикулярах.
МН - искомое расстояние.
АН = АВ√3/2 = 4√3.2 = 2√3 см как высота равностороннего треугольника.
Из ΔМАН по теореме Пифагора
МН = √(МА² + АН²) = √(4 + 12) = √16 = 4 см