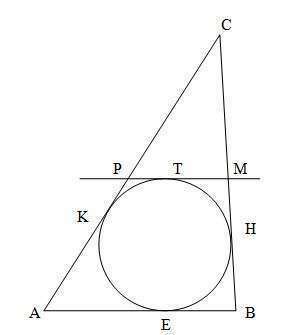
В ΔАВС вписана окружность. Е, Н, К - точки касания.
Заметим, что АЕ=АК, ВЕ=BH, CH=CK (как отрезки касательных проведенных из одной точки)
PM || АВ и касается окружности в точке Т.
РК=PT, MH=MT
Периметр Р(ΔАВС) = 2АВ + 2СК = 2(АВ+СК)
Пусть СК = х, тогда
2(АВ+х)=20
АВ+х=10, или АВ = 10-х
Периметр Р(ΔPMC) = CP+PT+TM+CM = CP+PК+MН+CM = СК+СН = х+х = 2х
ΔАВС и ΔРМС подобны ⇒ АВ/РМ = Р(АВС)/Р(РМС)
АВ/2.4 = 20/2х
АВ*х = 24
(10-х)х = 24
х²-10х+24=0
х₁ = 4; х₂ = 6
АВ = 6 или АВ = 4