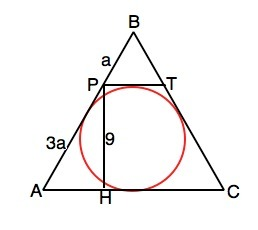
Примем коэффициент отношения ВР:АР равным а
Тогда ВР=а, АР=3а, АВ=4а
РТ║АС, АВ - секущая при них. ⇒
углы при основаниях ∆ АВС и ∆ ВРТ равны как соответственные, угол В общий. ⇒
∆ АВС~∆ ВРТ. ВР:АВ=1/4⇒
РТ:АС=1/4⇒
АС=4РТ
АРТС - трапеция. в неё вписана окружность. Вписать окружность в трапецию можно тогда и только тогда, когда сумма её оснований равна сумме боковых сторон. ⇒
РТ+АС=АР+ТС=6а.
АС=6а-РТ
РТ:(6а-РТ)=1/4⇒
4РТ=6а-РТ
5РТ=6а—
РТ=1,2а
АС=4,8а
Опустим высоту РН. Высота равнобедренной трапеции делит большее основание на отрезки, больший из которых равен полусумме оснований, меньший – их полуразности.
АН =(АС-РТ):2=(4,8а-1,2а):2=1,8а
Из прямоугольного ∆ АРН по т.Пифагора найдем значение а.
АР²-АН²=РН²
9а²-3,24а²=81⇒
5,76а²=81⇒
а=√14,0625=3,75
Р=12а=45 см