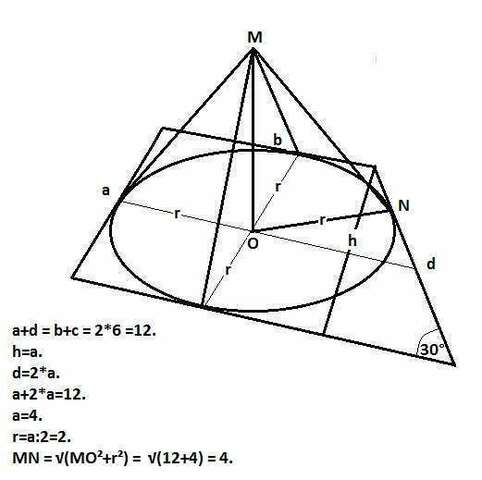
Раз точка М находится на равном расстоянии от СТОРОН трапеции, то это значит, что ее проекция является центром вписанной в эту трапецию окружности. А мы знаем, что в этом случае сумма боковых сторон трапеции равно сумме оснований (свойство трапеции). Сумма оснований нам дана, она равна 12. Заметим, что одна из боковых сторон трапеции (перпендикулярная основаниям) является диаметром вписанной окружности. Нам также дан острый угол = 30°. Опустим высоту из тупого угла на большее основание. В полученном прямоугольном треугольнике гипотенуза (наклонная боковая сторона) равна удвоенной второй стороне (высоте трапеции), так как высота лежит против угла 30°. Имеем уравнение: a+2*a=12, откуда а=4 (а - сторона, равная высоте и равная диаметру вписанной окружности). Точка М находится на расстоянии 2√3 от плоскости трапеции. Имеем прямоугольный треугольник с гипотенузой - искомым расстоянием и катетами 2√3 и 2 (радиус окружности). Отсюда по Пифагору искомое расстояние равно √(12+2) = 4.
Ответ: расстояние от точки М до сторон трапеции равно 4.