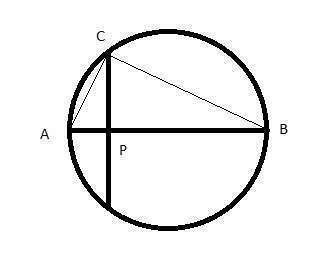
Диаметр перпендикулярный хорде делит ее на равные отрезки.
Рассмотрим треуг АСВ. В нем угол С - прямой, так как опирается на диаметр.
СР - высота, проведенная к гипотенузе - пропорциональна проекциям катетов на гипотенузу:
СР = √(6*24)=12 см
Хорда равна 2*СР=24 см.