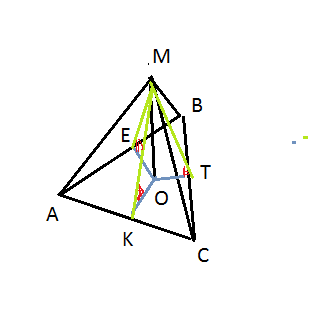
Правильная треугольная пирамида- в основании равносторонний треугольник.
Так как боковые грани наклонены к плоскости основания под углом альфа, тоапофемы боковых граней имеют равные проекции, поэтому О- центр вписанной окружности.
Треугольники МОК,МОТ,МЕТ
ОК=ОЕ=ОТ=r и r=l
Радиус вписанной окружности выражается через сторону а правильного треугольника АВС:
![r= \frac{a \sqrt{3} }{6}\Rightarrow a= \frac{6r}{ \sqrt{3} }=2r\cdot \sqrt{3}=[r=l]=2l \sqrt{3} r= \frac{a \sqrt{3} }{6}\Rightarrow a= \frac{6r}{ \sqrt{3} }=2r\cdot \sqrt{3}=[r=l]=2l \sqrt{3}](https://tex.z-dn.net/?f=r%3D+%5Cfrac%7Ba+%5Csqrt%7B3%7D+%7D%7B6%7D%5CRightarrow+a%3D+%5Cfrac%7B6r%7D%7B+%5Csqrt%7B3%7D+%7D%3D2r%5Ccdot+%5Csqrt%7B3%7D%3D%5Br%3Dl%5D%3D2l+%5Csqrt%7B3%7D+++)
В прямоугольном треугольнике МКО угол МКО равен α, значит МК=КО/cosα=l/cosα
S (бок)=3S(ΔAMC)=3·aMK/2=3·2l√3·l/cosα=6l²√3/cosα