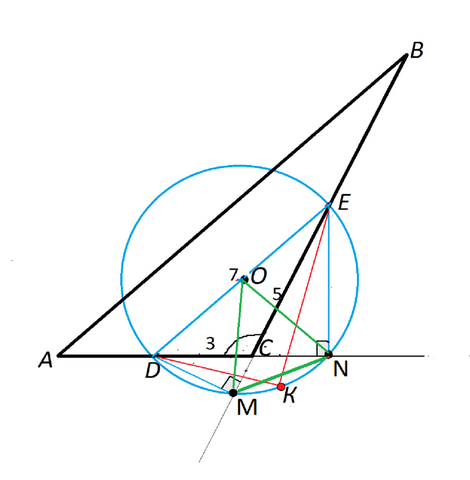
Сделаем рисунок.Так как окружность пересекает продолжения сторон АС и ВС, а точки N и М лежат на ней, углы DNЕ и DМЕ, опирающиеся на диаметр DE, - прямые, а угол DСЕ , вершина С которого находится внутри окружности, тупой.Поскольку точки D и Е - середины сторон АС и ВС, отрезок DЕ - средняя линия треугольника АВС и равен половине АВDЕ=АВ:2=7DС= АС:2=3СЕ=ВС:2=5Найдем величину угла DСЕ по т. косинусов. Вычисления давать не буду, ничего сложного в них нет.Главное, что найденный в результате косинус угла DСВ равен - 0,5, и этокосинус 120°.Угол ЕСN, как смежный с углом ЕСD, равен 60°.Т.к. треугольник ЕСN прямоугольный, угол СЕN равен 90°-60°=30°.На том же основании угол СDМ =30°Оба эти угла опираются на дугу МN.На ту же дугу опирается центральный угол МОN.Центральный угол, опирающийся на ту же дугу, что и вписанный, вдвое больше него, ⇒ угол МОN=60°.Угол ЕСN - внешний угол при вершине С треугольника DЕС. Он равен 60°, сумма углов ЕDС и DЕС равна этому внешнему углу и равна 60°.Сумма половин углов СЕN и СDМ равна 2*(30°:2)=30°. Следовательно, сумма углов ЕDК+КЕD равна 60°+30°=90°.Отсюда угол DКЕ равен 180°-90°=90°Треугольник DKE- прямоугольный, две его вершины лежат на окружности, а половина гипотенузы - радиус этой окружности.Следовательно, этот треугольник вписан в окружность, и К, точка пересечения биссектрис углов МЕNи NDМ, лежит на этой окружности, что и требовалось доказать. ——Треугольник МОN - равноберенный, т.к. ОМ=ОN= радиусу.Если угол при вершине равнобедренного треугольника равен 60°, этот треугольник - равносторонний.МN равна радиусу окружности, т.е. равна половине ее диаметра DЕМN=7:2=3,5