1. Диагонали ромба KMNP пересекаются в точке О. Найдите углы треугольника КОМ, если угол...

Question

1. Диагонали ромба KMNP пересекаются в точке О. Найдите углы треугольника КОМ, если угол MNP равен 80°.
2. На стороне ВС параллелограмма ABCD взята точка М так, что АВ = ВМ. а) Докажите, что AM – биссектриса угла BAD. б) Найдите периметр параллелограмма, если CD = 8 см, СМ = 4 см.

Answer 1

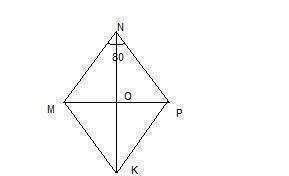
1. Диагонали ромба взаимно перпендикулярны и делят его углы пополам. ЗначитЗная, что сумма острых углов прямоугольного треуг-ка КОМ равна 90°, находим угол КМО:

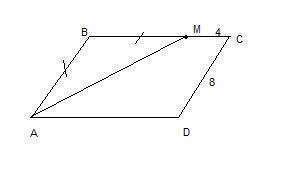
2 а). Рассмотрим треугольник АВМ. Он равнобедренный по условию (АВ=ВМ), значит, углы при его основании АМ равны между собой:
б). Поскольку АВ=ВМ=8 см, то ВС=8+4=12 см
Р = 2АВ+2ВС=2*8+2*12=40 см

---

---