Функция y = sin xГрафиком функции является синусоида.Полную неповторяющуюся часть синусоиды называют волной синусоиды.
Половину волны синусоиды называют полуволной синусоиды (или аркой).
Свойства функции y = sin x:1) Область определения функции – множество действительных чисел.2) Область значений функции – отрезок [–1; 1]3) Это нечетная функция.4) Это непрерывная функция.5) Координаты точек пересечения графика:
- с осью абсцисс: (πn; 0),
- с осью ординат: (0; 0).6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает.7) На промежутках [2πn; π + 2πn] функция принимает положительные значения.
На промежутках [-π + 2πn; 2πn] функция принимает отрицательные значения.8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn].
Промежутки убывания функции: [π/2 + 2πn; 3π/2 + 2πn].9) Точки минимума функции: -π/2 + 2πn.
Точки максимума функции: π/2 + 2πn10) Функция ограничена сверху и снизу. Наименьшее значение функции –1,
наибольшее значение 1.11) Это периодическая функция с периодом 2π (Т = 2π) Для построения графика функции y = sin x удобно применять следующие масштабы:- на листе в клетку за единицу отрезка примем длину в две клетки.
- на оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π. Это значения x.- на оси y отметим 1, включающий две клетки.
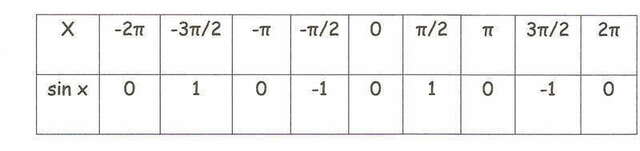
Составим таблицу значений функции, применяя наши значения x:
0
Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1). Это график функции y = sin x на отрезке [0; π]. Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна. Это график функции y = sin x на отрезке [-π; π].Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.