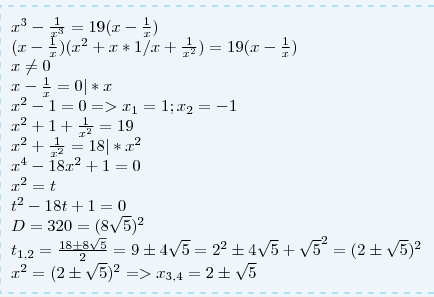x_1=1;x_2=-1 \\ x^2+1+ \frac{1}{x^2}=19 \\
x^2+ \frac{1}{x^2}=18|*x^2 \\ x^4-18x^2+1=0 \\ x^2=t \\ t^2-18t+1=0 \\ D=320=(8 \sqrt{5} )^2 \\ t_{1,2}= \frac{18 \pm 8 \sqrt{5}}{2}=9 \pm 4 \sqrt{5}=2^2 \pm 4 \sqrt{5}+ \sqrt{5}^2=(2 \pm \sqrt{5})^2 \\ x^2= (2 \pm \sqrt{5})^2 =>x_{3,4}=2 \pm \sqrt{5}" alt=" x^3- \frac{1}{x^3}=19( x- \frac{1}{x}) \\ (x- \frac{1}{x})(x^2+x*1/x+ \frac{1}{x^2})=19( x- \frac{1}{x}) \\ x \neq 0 \\ x- \frac{1}{x}=0|*x \\ x^{2} -1=0=>x_1=1;x_2=-1 \\ x^2+1+ \frac{1}{x^2}=19 \\
x^2+ \frac{1}{x^2}=18|*x^2 \\ x^4-18x^2+1=0 \\ x^2=t \\ t^2-18t+1=0 \\ D=320=(8 \sqrt{5} )^2 \\ t_{1,2}= \frac{18 \pm 8 \sqrt{5}}{2}=9 \pm 4 \sqrt{5}=2^2 \pm 4 \sqrt{5}+ \sqrt{5}^2=(2 \pm \sqrt{5})^2 \\ x^2= (2 \pm \sqrt{5})^2 =>x_{3,4}=2 \pm \sqrt{5}" align="absmiddle" class="latex-formula">