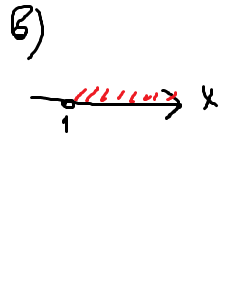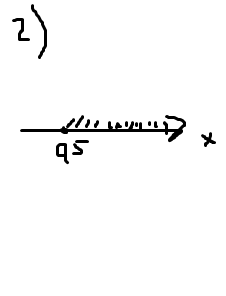Б)
Умножаем на (-1) все слагаемые.

Находим дискриминант.(D)
D = b²- 4*a*c= (-10)² -4*2*12= 100- 96=4. D >0.
Находим корни дискриминанта.


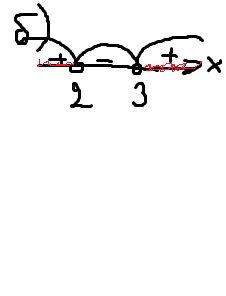
Рисуешь прямую координатную и отмечаешь на ней точки ( корни дискриминанта) т.е x1=3 и x2= 2. Выделяешь промежутки дугой, а для того чтобы узнать знак промежутка подставляешь в уравнение
 , x1=3 и x2= 2 ⇒
, x1=3 и x2= 2 ⇒
 , смотрим на коорд. прямую на промежуток от (3 до = + бесконечности). Возьмём любое число, которое больше 3-х , например - 6 и подставим в уравнение ⇒
, смотрим на коорд. прямую на промежуток от (3 до = + бесконечности). Возьмём любое число, которое больше 3-х , например - 6 и подставим в уравнение ⇒  . В первой скобке при вычитании 6-3, получается 3 , знак у этого числа - положительный. Во второй 6-2 получается 4, знак положительный ⇒ этот промежуток положительный.
. В первой скобке при вычитании 6-3, получается 3 , знак у этого числа - положительный. Во второй 6-2 получается 4, знак положительный ⇒ этот промежуток положительный.
Рассмотрим промежуток ( - бесконечности до 2), так же подставляем в уравнение допустим -1, тогда получается  , -1-3 =-4 ; -1-2 =-3 при умножении минуса на минус получается плюс ⇒ этот промежуток положительный. Рассмотрим промежуток от (2;3). Возьмем и подставим в уравнение число 2,5, тогда
, -1-3 =-4 ; -1-2 =-3 при умножении минуса на минус получается плюс ⇒ этот промежуток положительный. Рассмотрим промежуток от (2;3). Возьмем и подставим в уравнение число 2,5, тогда  2,5-3 =-0,5 ,а 2,5-2 =0,25 ;-0,5*0,5 = знак отрицательный ⇒ промежуток отрицательный. Т.к в нашем уравнении стоит знак ≥0, то нам надо всё, что больше 0 , т.е -положительное ⇒ Ответ : х∈( от - бесконечности до 2) U ( от 3 до + бесконечности).
2,5-3 =-0,5 ,а 2,5-2 =0,25 ;-0,5*0,5 = знак отрицательный ⇒ промежуток отрицательный. Т.к в нашем уравнении стоит знак ≥0, то нам надо всё, что больше 0 , т.е -положительное ⇒ Ответ : х∈( от - бесконечности до 2) U ( от 3 до + бесконечности).
Пример Г) - аналогичный. Только на -1 умножать не надо т.к первое слагаемое(а) положительное.
В)  0" alt="2 x^{2} +2>0" align="absmiddle" class="latex-formula">
0" alt="2 x^{2} +2>0" align="absmiddle" class="latex-formula">
 -2" alt="2 x^{2} >-2" align="absmiddle" class="latex-formula">
-2" alt="2 x^{2} >-2" align="absmiddle" class="latex-formula">
Делим -2 на 2 ( знак > - не меняется)
 -1" alt=" x^{2} > -1" align="absmiddle" class="latex-formula">
-1" alt=" x^{2} > -1" align="absmiddle" class="latex-formula">
 1" alt=" x>1" align="absmiddle" class="latex-formula">
1" alt=" x>1" align="absmiddle" class="latex-formula">
Рисуем коорд. прямую х. отмечаем 1, у нас стоит знак > ⇒ нам нужно всё, что больше 1
Ответ : х∈ ( от 1 до + бесконечности)
Д) так же как и В)

Снимаем квадрат.

1/2 =0,5
Рисуем коорд. прямую. ⇒ ×∈ (0,5 до + бесконечности)