Решаем первое уравнение системы
х²+3х-18=0
D=9-4·(-18)=81=9²
x₁=(-3-9)/2=-6 или х₂=(-3+9)/2=3
у₁=4-3х₁=4-3·(-6)=22 или у₂=4-3х₂=4-3·3=-5
Ответ.(-6;22) (3;-5)


t≠0
2t²-5t+2=0
D=(-5)²-4·2·2=25-16=9=3²
t=(5-3)/4=1/2 или t=(5+3)/4=2
Решаем две системы

Из первого уравнения
2(х+у)=х-y ⇒2x+2y=x-y ⇒ 2x-x=-2y-y ⇒ x=-3y
и подставим во второе
(-3у)²+у²=20 ⇒10у²=20 ⇒у²=2
у₁=-√2 или у₂=√2
х₁=-3у₁=-3·(-√2)=3√2 или х₂=-3у₂=-3·√2
б)

Из первого уравнения
х+у=2(х-y) ⇒x+y=2x-2y ⇒ х- 2x=-2y-y ⇒ x=3y
и подставим во второе
(3у)²+у²=20 ⇒10у²=20 ⇒у²=2
у₃=-√2 или у₄=√2
х₃=3у₃=3·(-√2)=-3√2 или х₄=3у₄=3·√2
Ответ. (3√2;-√2) ;(-3√2;√2) ;(-3√2;-√2) ;(3√2;√2)

2} \atop {2(3x-2)-5(6-x) \geq 20x-70}} \right. " alt="3) \left \{ {{ x^{2} -7>2} \atop {2(3x-2)-5(6-x) \geq 20x-70}} \right. " align="absmiddle" class="latex-formula">
Умножили первое неравенство на 2, второе на 10

0} \atop {6x-4-30+5x \geq 20x-70}} \right. \\ \left \{ {{ (x-3)(x+3)>0} \atop {-9x \geq -36}} \right. \\ \left \{ {{ (x-3)(x+3)>0} \atop {x \leq 4}} \right." alt=" \left \{ {{ x^{2} -9>0} \atop {6x-4-30+5x \geq 20x-70}} \right. \\ \left \{ {{ (x-3)(x+3)>0} \atop {-9x \geq -36}} \right. \\ \left \{ {{ (x-3)(x+3)>0} \atop {x \leq 4}} \right." align="absmiddle" class="latex-formula">
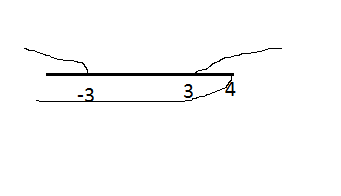
cм. рис.
Ответ. (-∞;-3)U(3;4]