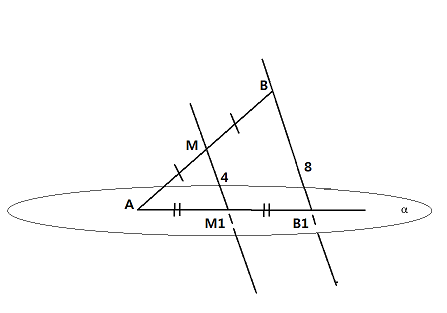
Смотри рисунок к задаче в прикрепленном файле.
1) Так как M1B1 || BB1 значит можно провести плоскость β (по теореме, через параллельные прямые можно провести плоскость, и при том только одну).
М є ММ1, М є АВ => M є β
В є ВВ1, В є АВ => B є β
Следовательно, отрезок АВ будет лежать в β плоскости, потому как уже А и В точки его принадлежат плоскости.
α пересекает β по M1B1, AB є β => A, M1, B1 лежат на общей прямой пересечения плоскостей α и β
2) ΔАММ1 ~ ΔABB1 по 3ему признаку (за 3мя углами). Следовательно, выполняется следующее отношение: