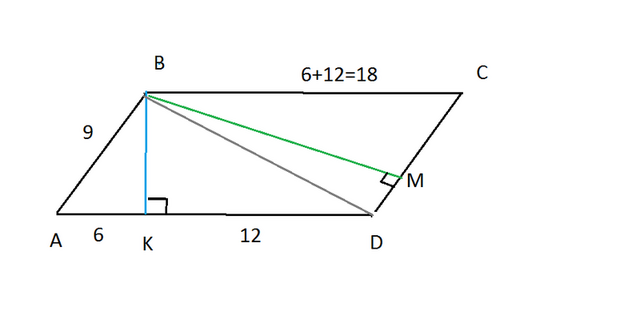
1) Из прямоугольного треугольника АВК по теореме Пифагора
ВК² = АВ² - АК² = 9² - 6² = 45 ⇒ ВК = 3√5
2) Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне
Сторон две, высот тоже две. Площадь одна и та же
Поэтому
AD·BK = CD·BM
18·3√5=9·BM ⇒ BM = 6√5
3) Из прямоугольного треугольника ВМС:
МС²=BC²-BM²=18²-(6√5)²=324-36·5=324-180=144=12²
MC=12
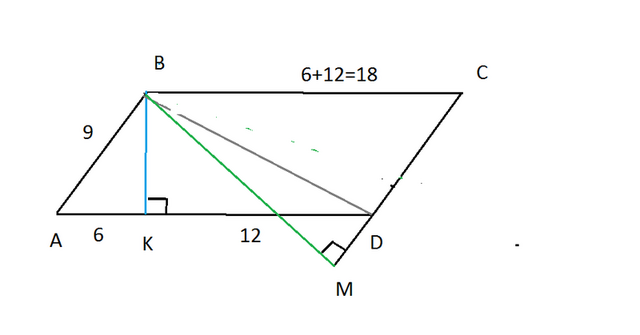
Но так как СD=9, а проекция ВС равна 12, значит точка М не лежит на стороне CD.
Поэтому рисунок будет таким как на втором приложении
Треугольники DBK и DBM не могут быть подобными
так как катеты певрого 3√5 и 12, второго 6√5 и 3=12-9
Стороны не пропорциональны.