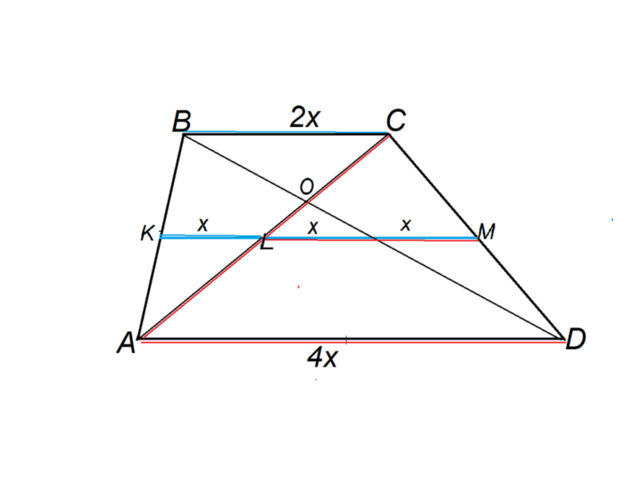
Диагонали трапеции делят среднюю линию на три равные части. Как относятся основания?
Рассмотрим рисунок, данный в приложении.
В трапеции АВСД отрезок КМ - средняя линия.
Пусть каждый отрезок, получившийся при пересечении средней линии диагоналями, равен х.
В треугольнике АВС отрезок КL- средняя линия, т.к. АК=КВ, КL|| BC
BC=2KL=2x
В треугольнике АСD отрезок LM=2x.
Т.к. LM- средняя линия треугольника АСD, AD=2LM=4x
AD:BC=4х:2х=2:1
Отношение оснований равно 2:1