1. Область определения функции

- множество всех действительных чисел.
2. Исследовать на четность

Итак, функция ни четная ни нечетная.
3. Функция не пертодическая
4. Точки пересечения с осью Ох и Оу
4.1. Точки пересечения с осью Ох

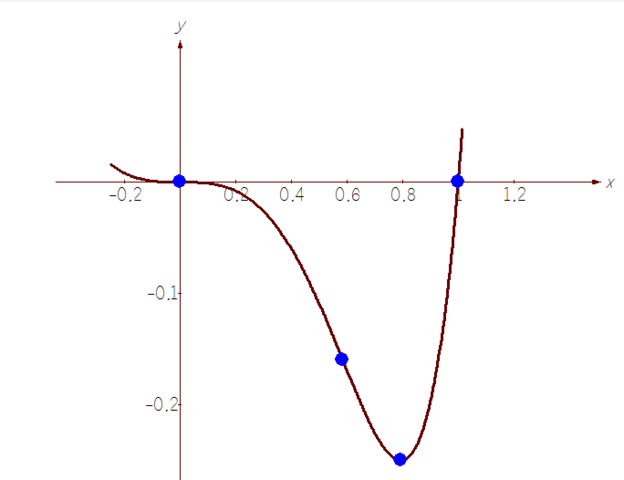
(0;0), (-1;0) - точки пересечения с осью Ох
4.2. Точки пересечения с осью Оу

(0;0) - точки пересечения с осью Оу.
5. Критические точки, возрастание и убывание функции
5.1
![y'=6x^5-3x^2 \\ 3x^2(2x^3-1)=0 \\ x_1=0 \\ x_2= \frac{ \sqrt[3]{4} }{2} y'=6x^5-3x^2 \\ 3x^2(2x^3-1)=0 \\ x_1=0 \\ x_2= \frac{ \sqrt[3]{4} }{2}](https://tex.z-dn.net/?f=y%27%3D6x%5E5-3x%5E2+%5C%5C+3x%5E2%282x%5E3-1%29%3D0+%5C%5C+x_1%3D0+%5C%5C+x_2%3D+%5Cfrac%7B+%5Csqrt%5B3%5D%7B4%7D+%7D%7B2%7D+)
Итак, функция возрает на промежутке
![( \frac{ \sqrt[3]{4} }{2} ;+\infty) ( \frac{ \sqrt[3]{4} }{2} ;+\infty)](https://tex.z-dn.net/?f=%28+%5Cfrac%7B+%5Csqrt%5B3%5D%7B4%7D+%7D%7B2%7D+%3B%2B%5Cinfty%29)
, убывает -

В точке х = ∛4/2 - функция имеет локальный минимум. а в точке х=0 - локальный максимум
6 Возможные точки перегиба
![y''=30x^4-6x \\ 6x(5x^3-1)=0 \\ x_1=0 \\ x_2= \frac{ \sqrt[3]{25} }{5} y''=30x^4-6x \\ 6x(5x^3-1)=0 \\ x_1=0 \\ x_2= \frac{ \sqrt[3]{25} }{5}](https://tex.z-dn.net/?f=y%27%27%3D30x%5E4-6x+%5C%5C+6x%285x%5E3-1%29%3D0+%5C%5C+x_1%3D0+%5C%5C+x_2%3D+%5Cfrac%7B+%5Csqrt%5B3%5D%7B25%7D+%7D%7B5%7D+)