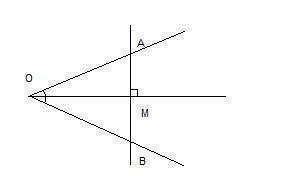
Имеется два прямоугольных треугольника АМО и ВМО. Эти треугольники равны по одному из признаков равенства прямоугольных треуг-ов: если катет и прилежащий к нему острый угол одного прямоугольного треуг-ка соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. В нашем случае ОМ - общий катет, а углы АОМ и ВОМ равны, поскольку ОМ - биссектриса. У равных треугольников равны и соответственные стороны АМ и ВМ.