№2. Диагонали прямоугольника равны и в точке пересечения делятся пополам.
Треугольник АОВ - равнобедренный, так как АО=ОВ
Значит ∠ОАВ= ∠
ОВА=(180°-80°)/2=50°
№ 4
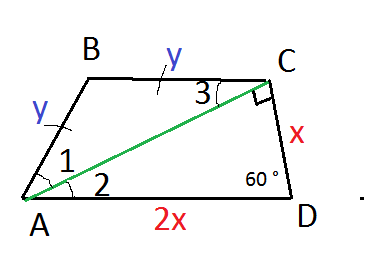
См. рисунок.
В прямоугольном треугольнике АСD дан один острый угол 60°, значит второй острый угол 30°.
Против угла в 30° катет равен половине гипотенузы.
Обозначим CD=x, тогда AD= 2x
Так как АС - биссектриса, то она делит угол А пополам.
∠1=∠2
∠2=∠3 - внутренние накрест лежащие при параллельных прямых ВС и AD и секущей АС.
Значит 1=∠3, треугольник АВС - равнобедренный
АВ=ВС=у
Периметр трапеции - это сумма всех сторон
АВ+ВС+СD+AD=35 cм
у+у+x + 2x = 35
2y+3x=35
Дальше однозначного решения нет,
но если трапеция равнобедренная и у=х
то
х+х+х+2х=35
5х=35
х=7
AB=7