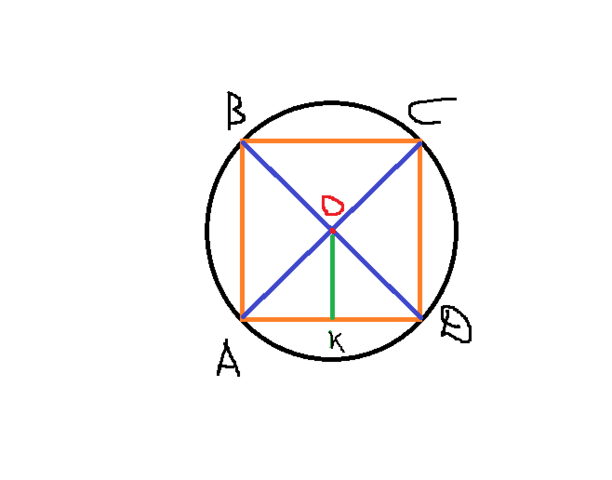
В окружность вписан четырех угольник.... но можно сформулировать и по другому - окружность описывает четырехугольник.
вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°. из всех параллелограммов только около прямоугольника и квадрата можно описать окружность. ее центр лежит на пересечении диагоналей. но поскольку диагонали у нас по условию перпендикулярны, то четырехугольник - квадрат.
смотри рисунок во вложении
Δ ABC - прямоугольный и равнобедренный
высота OA = 1/2 диагонали AC
Δ AOD - прямоугольный и равнобедренный
высота OK - совпадает с биссектрисой и медианой ⇒ OK= 1/2 BC