Ответы к задачам с подобным условием даны здесь не раз.
Эта задача решена мною неделю назад.
Вот это решение:
Углы при одном из оснований трапеции равны 86 и 4, а отрезк, соединяющие середины противоположных сторон трапеции, равны 4 и 1. Найдите основания трапеции.
Сделаем рисунок.
Отрезок, соединяющий боковые стороны трапеции - ее средняя линия.
Ее рисовать не будем, - не пригодится.
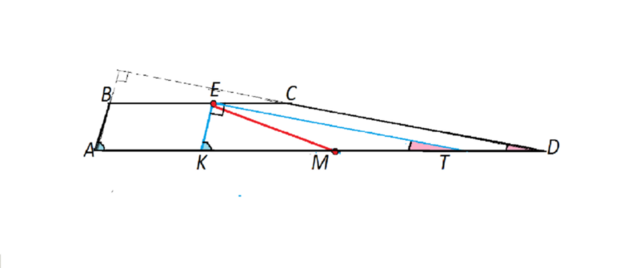
Отрезок, соединяющий середины оснований, обозначим ЕМ.
Из Е к АD проведем отрезки ЕК и ЕТ, параллельные соответственно АВ и СD. Тогда АК=ВЕ, а ЕС=ТD как стороны параллелограммов АВЕК и ЕСDМ - стороны в них попарно параллельны и равны.
Углы при основании получившегося треугольника КЕМ равны 86° и 4°, так как равны углам трапеции при АD по свойству параллельных прямых.
Обратим внимание на то, что сумма углов при основании АD равна 86+4=90°, следовательно, угол Е=90°, и треугольник КЕТ - прямоугольный.
ВЕ=ЕС,⇒ АК=ТD, а так как М - середина АD, то КМ=МТ.
ЕМ - медиана ⊿КЕТ, и по свойству медианы прямоугольного треугольника гипотенуза КТ=2ЕМ
ЕМ=1 по условию,
КТ=2
Пусть ВЕ=х. Тогда и ЕС=АК=ТД=х
Сумма оснований равна двум средним линиям трапеции.
ВС+АД=4*2=8.
ВЕ+ЕС+АК+ТД=4х
ВС+АД=8
4х+КТ=8
4х+2=8
4х=6
х=1,5.
ВС=1,5*2=3
АД=8-3=5
Ответ: основания раны 3 и 5
------------
[email protected]