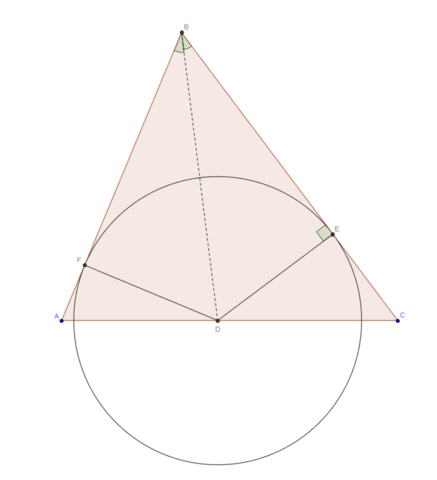
Понятно, что центр окружности должен лежать на биссектрисе угла (вспоминая, что биссектриса - ГМТ точек, равноудаленных от сторон угла). Тогда можно найти длину биссектрисы, угол и затем получить длину радиуса как катет в прямоугольном треугольнике.
Поступим иначе. Отразим треугольник относительно AC. Искомая окружность будет вписана в получившийся дельтоид, следовательно, будет связь между радиусом окружности, полупериметром дельтоида и площадью дельтоида: Sд = pд * r
Площадь дельтоида равна удвоенной площади треугольника, которую можно найти по формуле Герона (S = sqrt(p * (p - a) * (p - b) * (p - c)) = sqrt(21 * 6 * 7 * 8) = 84). А полупериметр дельтоида равен 13 + 15 = 28. Тогда
r = 2 * 84 / 28 = 6