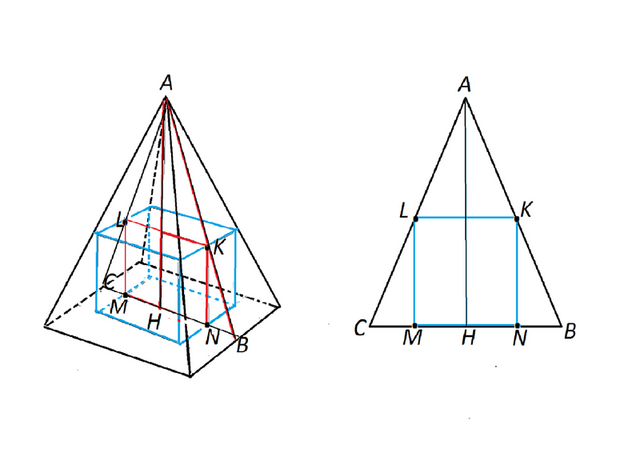
В правильную четырехугольную пирамиды вписан куб. Найдите ребро куба, если высота пирамиды 60, сторона основания пирамиды 40
-----
Основание куба лежит на основании пирамиды,
а точка пересечения диагоналей основания совпадет с основанием высоты пирамиды.
Верхняя грань куба является сечением пирамиды, параллельным её основанию.
Проведем через высоту пирамиды сечение перпендикулярно основанию.
Это сечение пройдет и по середине куба.
Длина сторон вертикального сечения куба равна длине его ребер.
Сделаем рисунок этого сечения.
Это сечение -
равнобедренный треугольник. АВС
АВ=АС, ВС - основание, АН-. высота
Сечение куба - квадрат KLMN
Треугольник АНВ прямоугольный с катетами АН=60 и НВ=20.
LK=KN=NM=ML- стороны сечения куба, равные его ребрам.
∆ АНВ~∆ KNB (по равным углам при АН║KN и секущей АВ)
Пусть
KN - сторона квадрата KLMN -
равна х, тогдa
NH =0,5х.
Из подобия треугольников:
АН:KN=HB:NB
NB=HB-HN=
20-0,5х
60:х=20:(20-0,5х)
1200-30х=20х
1200=50х
х=24
Ответ: ребро куба равно 24
-------
[email protected]