Выучить определения:
f(-x)=f(x) четная, значения равны при изм. знака аргумента на противоположный
f(-x)=-f(x) нечетная, значения равны, но противоположны по знаку, при изм. знака ар.
посмотреть как выглядят их графики:
чётная - симметрична относительно оси "у"
нечетная -симметрична отн. начала координат, поворот на 180 градусов
можно использовать свойства суммы, произведения четных, нечётных функций (см.учебник)
дальше решаем:
у=х+3 у=|x+1| чётностью не обладают
раскрыть знаки модуля и определить вид функции на интервалах
|x-1| равен х-1 при х больше 1, -(х-1) при х меньше 1
|x+1| равен х+1 при х больше -1, -(х+1) при х меньше -1
Т.о. получаем три различных интервала:
меньше -1
от -1 до 1
больше 1
определим вид функции на каждом интервале, для чего раскроем скобки и приведем подобные члены:
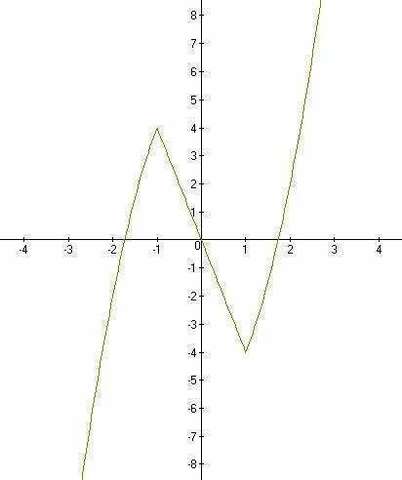
а) меньше -1 у=(х+3)(1-х)+(х-3)(-х-1)= -2x^2+6
б) от -1 до 1 у=(х+3)(1-х)+(х-3)(х+1)= -4х
в) больше 1 у=(х+3)(х-1)+(х-3)(х+1)=2x^2-6
Т.о. -4х нечётная, 2x^2-6 = -( -2x^2+6) тоже нечётная, на всех интервалах функция нечетная
второй пример уж самостоятельно, всё тоже самое