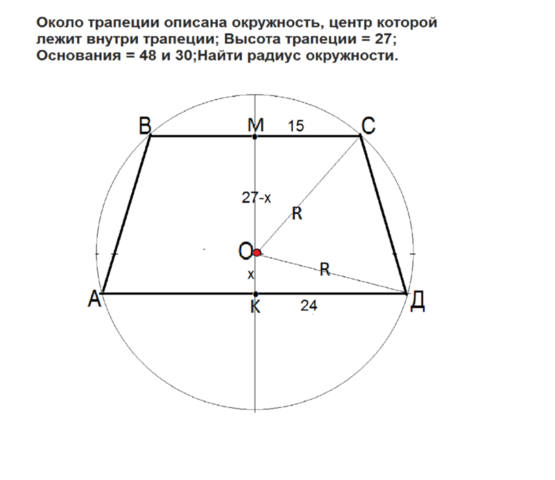
Около трапеции описана окружность - значит, трапеция вписанная и равнобедренная, т.к. в окружность можно вписать только равнобедренную трапецию.
Сделаем рисунок, обозначим вершины углов трапеции привычными АВСД Через центр окружности проведем перпендикулярно к основаниям трапеции диаметр.
Его отрезок МК, заключенный между основаниями трапеции, является ее высотой и делит основания пополам. ( Основания - хорды, перпендикуляр из центра окружности к хорде делит ее пополам).
Соединим центр О с вершинами С и Д.
ОС=ОД=R
Обозначим ОК=х, тогда ОМ =27-х
По т. Пифагора
R²=МС²+ОМ²
R²=КД²+ОК² Приравняем значения радиуса.
МС²+ОМ²=КД²+ОК²
225+(27-х)²=576+х²
54х=378
х=7
ОК=7
R²=КД²+ОК²
R²=24²+7²
R²=625
R=25