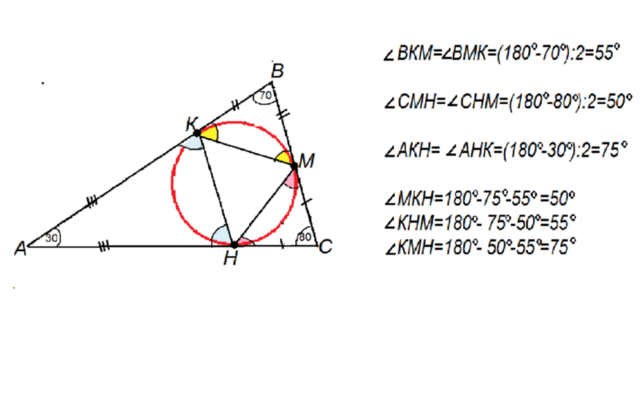
В треугольник с углами 30°, 70°, 80° вписана окружность. Найти углы треугольника, вершинами которого являются точки касания вписанной окружности и сторон данного треугольника.
Решение.
Обозначим вершины исходного треугольника АВС, точки касания окружности и сторон треугольника - КМН.
См. рисунок.
По свойству отрезков касательных, проведенных из одной точки к окружности, треугольники КАН, МСН и КВМ - равнобедренные.
Сумма углов треугольника равна 180°
В треугольнике КАН углы при КН равны по (180°-30°):2=75°
В треугольнике КВМ углы при КМ равны по 55° ( на том же основании)
В треугольнике МСН углы при МН равны по 50°
Угол АКВ развернутый.
Угол НКМ равен разности между развернутым углом АКВ и суммой смежных с ним углов. Он равен 50°
На таком же основании
Угол КМН=75°
Угол МНК=55°