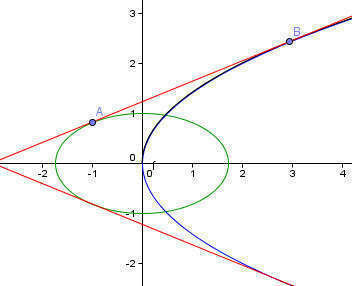
x^2/3+y^2/1=1. y^2=2x.
Выразим из каждого уравнения у и найдем их производную


Пусть (x₁;y₁) - координаты точки касания на первой линии, (x₂;y₂) - на второй. Получим уравнение касательной для первой и второй линий.
Поскольку производная равна угловому коэффициенту касательной, то для общей касательной выполняется равенство производных

Общий вид уравнения касательной:
y=f(x₀)+f '(x₀)(x-x₀)

Т.к. речь идет об одной и той же касательной, то



Тогда искомое уравнение

Если f(x₀)>0, то и k>0. Второй полученный корень не рассматриваем, т.к. при этом знаменатель обращается в 0